🔌 Circuits et Filtres Analogiques - S5
Année: 2022-2023 (Semestre 5)
Crédits: 3 ECTS
Type: Électronique Analogique
PART A: PRÉSENTATION GÉNÉRALE
Objectifs du cours
Le cours “Circuits et Filtres Analogiques” fournit une compréhension approfondie de l’analyse et de la conception de circuits électroniques analogiques, avec un accent particulier sur la théorie des filtres. Il couvre l’utilisation des amplificateurs opérationnels, l’analyse fréquentielle via les diagrammes de Bode, et l’analyse temporelle via la transformée de Laplace. Ce cours est fondamental pour la conception de chaînes d’acquisition de signaux, le conditionnement de capteurs, et le traitement analogique du signal.
Compétences visées
- Maîtriser l’analyse fréquentielle des circuits (diagrammes de Bode, fonction de transfert)
- Concevoir des filtres actifs et passifs (passe-bas, passe-haut, passe-bande)
- Utiliser les amplificateurs opérationnels dans diverses configurations
- Appliquer la transformée de Laplace pour l’analyse temporelle
- Dimensionner des circuits analogiques pour des applications spécifiques
- Simuler et valider des circuits avec LTspice
- Analyser les systèmes du 1er et 2ème ordre
Organisation
- Volume horaire: 36h (CM: 20h, TD: 8h, TP: 8h)
- Évaluation: Examen écrit (60%) + TDs/TPs (30%) + Contrôle continu (10%)
- Semestre: 5 (2022-2023)
- Prérequis: Électronique fondamentale, mathématiques (nombres complexes, dérivées, intégrales)
PART B: EXPÉRIENCE, CONTEXTE ET FONCTION
Contenu pédagogique
Le cours s’articule autour de trois grandes parties couvrant les aspects théoriques et pratiques de l’électronique analogique.
1. Amplificateurs Opérationnels et Montages de Base
Amplificateur Opérationnel Idéal:
L’amplificateur opérationnel (AO ou op-amp) est le composant fondamental de l’électronique analogique moderne.
Caractéristiques de l’AO idéal:
- Gain en tension différentiel infini: Ad = ∞
- Impédance d’entrée infinie: Zin = ∞ (courants d’entrée nuls)
- Impédance de sortie nulle: Zout = 0
- Bande passante infinie
- Tension de décalage (offset) nulle
- Rejet du mode commun infini (CMRR = ∞)
Règles de l’AO idéal en régime linéaire (contre-réaction négative):
- V+ = V- (égalité des tensions d’entrée)
- I+ = I- = 0 (courants d’entrée nuls)
Montages fondamentaux:
Amplificateur inverseur:
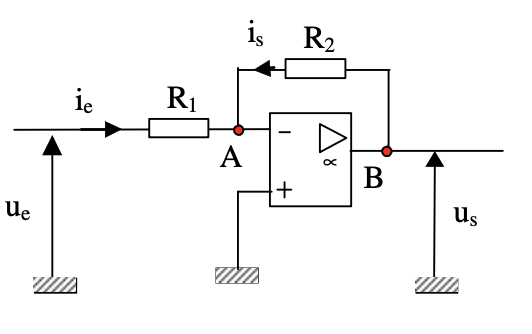

Amplificateur non-inverseur:
R2
----/\/\/----
| |
+-[AO+]-----+---- Vs
| | -|
Ve --+ | |
R1 |
\ |
\ |
GND
Fonction de transfert: H = Vs/Ve = 1 + (R2/R1)
Impédance d’entrée: Zin = ∞ (très élevée)
Suiveur (buffer): Configuration non-inverseuse avec R2 = 0 et R1 = ∞
H = 1
Utilisé pour adapter les impédances (isolation).
Sommateur inverseur:
Ve1 -R1-\
Ve2 -R2--+-[AO-]---- Vs
Ve3 -R3-/ | +|
R4 |--- GND
Vs = -R4 × (Ve1/R1 + Ve2/R2 + Ve3/R3)
Si R1 = R2 = R3 = R4 = R: Vs = -(Ve1 + Ve2 + Ve3)
Soustracteur (amplificateur différentiel):
Ve1 -R1--[AO-]---R2--- Vs
| +|
Ve2 -R3--+ |
R4 |
\ |
GND
Si R1 = R2 et R3 = R4: Vs = (R2/R1) × (Ve2 - Ve1)
Intégrateur:
C
----||----
| |
Ve -R1-[AO-]-+---- Vs
| +|
| |--- GND
Vs(t) = -(1/(R×C)) × ∫Ve(t)dt + Vs(0)
En fréquentiel: H(jω) = -1/(jRCω)
Dérivateur:
R2
----/\/\/----
| |
Ve -C1-[AO-]----+---- Vs
| +|
| |--- GND
Vs(t) = -RC × dVe(t)/dt
En fréquentiel: H(jω) = -jRCω
Supports de cours:
2. Fonctions de Transfert et Analyse Fréquentielle
Fonction de transfert:
La fonction de transfert H(jω) d’un système linéaire relie la sortie à l’entrée en régime harmonique:
H(jω) = Vs(jω)/Ve(jω)
où j = √(-1) et ω = 2πf (pulsation en rad/s)
Module et phase: H(jω) = |H(jω)| × exp(jφ(ω))
-
Module (gain): H(jω) , souvent exprimé en décibels (dB) GdB = 20 × log10( H(jω) ) - Phase: φ(ω) = arg(H(jω)), exprimée en degrés ou radians
Diagramme de Bode:
Représentation graphique de la fonction de transfert:
- Diagramme de gain: GdB en fonction de log(f)
- Diagramme de phase: φ en fonction de log(f)
Filtres du 1er ordre:
Filtre passe-bas RC passif:
Ve ---R---+--- Vs
|
C
|
GND
Fonction de transfert: H(jω) = 1/(1 + jRCω) = 1/(1 + j(ω/ω0))
où ω0 = 1/(RC) est la pulsation de coupure.
Fréquence de coupure à -3dB: f0 = 1/(2πRC)
Comportement asymptotique:
- Basses fréquences (ω « ω0): H ≈ 1 → 0 dB
- Hautes fréquences (ω » ω0): H ≈ ω0/ω → pente -20 dB/décade
Phase: φ(ω) = -arctan(ω/ω0)
À la fréquence de coupure: φ(ω0) = -45°
Filtre passe-haut CR passif:
Ve ---C---+--- Vs
|
R
|
GND
Fonction de transfert: H(jω) = (jRCω)/(1 + jRCω) = j(ω/ω0)/(1 + j(ω/ω0))
Filtres du 2ème ordre:
Forme canonique: H(p) = (H0 × ω0²)/(p² + (ω0/Q)×p + ω0²)
où:
- p = jω (variable de Laplace en régime harmonique)
- ω0: pulsation propre (ou pulsation de résonance)
- Q: facteur de qualité
- H0: gain statique
Facteur de qualité Q (ou coefficient d’amortissement ξ = 1/(2Q)):
- Q < 0.5 (ξ > 1): système suramort (pas de dépassement)
- Q = 0.5 (ξ = 1): amortissement critique
- Q = 0.707 (ξ = 0.707): réponse de Butterworth (maximalement plate)
- Q > 0.707: système sous-amorti (dépassement, résonance)
Filtre passe-bas du 2ème ordre (Sallen-Key):
Ve -R1--+--R2--+-----[AO+]---- Vs
| | | -|
C1 C2 +---+
| | |
GND GND R3
|
R4
|
GND
Pour un filtre de Butterworth (Q = 0.707), configuration unitaire:
H(jω) = 1/(1 + √2 × j(ω/ω0) - (ω/ω0)²)
Pente de coupure: -40 dB/décade (2 × 20 dB/décade)
Quadripôles:
Un quadripôle est un système à 2 ports (entrée et sortie) caractérisé par des matrices de transfert.
Matrice impédance [Z]: [V1] [Z11 Z12] [I1] [V2] = [Z21 Z22] [I2]
Matrice admittance [Y] = [Z]⁻¹
Matrice de transmission (ABCD): [V1] [A B] [V2 ] [I1] = [C D] [-I2]
Avantage: pour des quadripôles en cascade, on multiplie les matrices ABCD.
Supports de cours:
3. Transformée de Laplace et Analyse Temporelle
Transformée de Laplace:
Outil mathématique permettant de transformer les équations différentielles en équations algébriques.
L{f(t)} = F(p) = ∫[0 à ∞] f(t) × exp(-pt) dt
où p = σ + jω est la variable complexe de Laplace.
Transformées usuelles:
| Signal temporel f(t) | Transformée F(p) |
|---|---|
| Échelon u(t) | 1/p |
| Impulsion δ(t) | 1 |
| Rampe t×u(t) | 1/p² |
| Exponentielle exp(-at)×u(t) | 1/(p+a) |
| Sinus sin(ωt)×u(t) | ω/(p² + ω²) |
| Cosinus cos(ωt)×u(t) | p/(p² + ω²) |
Propriétés de la transformée:
- Linéarité: L{a×f(t) + b×g(t)} = a×F(p) + b×G(p)
- Dérivation: L{df/dt} = p×F(p) - f(0⁻)
- Intégration: L{∫[0 à t] f(τ)dτ} = F(p)/p
- Théorème du retard: L{f(t-τ)×u(t-τ)} = exp(-pτ)×F(p)
- Théorème de la valeur initiale: f(0⁺) = lim[p→∞] p×F(p)
- Théorème de la valeur finale: f(∞) = lim[p→0] p×F(p)
Application aux circuits:
En transformée de Laplace, les éléments deviennent:
- Résistance: R (inchangée)
- Condensateur: impédance 1/(pC)
- Inductance: impédance pL
Exemple - Circuit RC:
Équation temporelle: RC × dVs/dt + Vs = Ve
En Laplace (conditions initiales nulles): RC × p×Vs(p) + Vs(p) = Ve(p)
Fonction de transfert: H(p) = Vs(p)/Ve(p) = 1/(1 + RCp)
Réponse temporelle d’un système du 2ème ordre:
Pour un système du 2ème ordre: H(p) = ω0²/(p² + 2ξω0×p + ω0²)
Réponse indicielle (entrée échelon):
-
Cas suramort (ξ > 1): deux pôles réels distincts, pas de dépassement
-
Cas critique (ξ = 1): pôle réel double, réponse la plus rapide sans dépassement
-
Cas sous-amorti (0 < ξ < 1): pôles complexes conjugués, oscillations amorties
Vs(t) = V0 × [1 - (exp(-ξω0×t)/√(1-ξ²)) × sin(ωd×t + φ)]
où ωd = ω0×√(1-ξ²) (pseudo-pulsation)
Dépassement (overshoot): D% = 100 × exp(-πξ/√(1-ξ²))
Pour Q = 0.707 (ξ = 0.707): D ≈ 4.3%
Temps de montée tm (10% à 90%): tm ≈ 2.2/ω0
Temps de réponse tr (à 5%): tr ≈ 3/(ξω0)
Circuits RLC:
Circuit RLC série:
Équation différentielle: L × d²i/dt² + R × di/dt + (1/C)×i = dVe/dt
En Laplace: H(p) = I(p)/Ve(p) = pC/(LCp² + RCp + 1)
Pulsation propre: ω0 = 1/√(LC)
Facteur de qualité: Q = (1/R)×√(L/C) = (ω0×L)/R
Analyse des signaux:
- Fonction de transfert harmonique: réponse en régime sinusoïdal permanent
- Réponse impulsionnelle: h(t) = L⁻¹{H(p)}
- Réponse indicielle: s(t) = L⁻¹{H(p)/p}
- Convolution: y(t) = h(t) * x(t) = ∫[-∞ à ∞] h(τ)×x(t-τ) dτ
Supports de cours:
PART C: ASPECTS TECHNIQUES
Cette section présente les travaux pratiques et exercices réalisés.
Travaux Pratiques avec LTspice
TP1: Cellules CR et RC
Objectif: Étude des filtres passifs du 1er ordre et validation par simulation.
Cellule RC (Passe-Bas):
Schéma simulé dans LTspice:
Circuit RC passe-bas:
V1 (AC source) --- R1 (1kΩ) ---+--- Vout
|
C1 (100nF)
|
GND
Calcul théorique: f0 = 1/(2π×RC) = 1/(2π × 1000 × 100×10⁻⁹) = 1.59 kHz
Simulation:
- Analyse AC de 10 Hz à 100 kHz
- Tracé du diagramme de Bode (gain et phase)
- Vérification de la fréquence de coupure à -3 dB
- Pente de -20 dB/décade après f0
Cellule CR (Passe-Haut):
Circuit CR passe-haut:
V1 (AC source) --- C1 (100nF) ---+--- Vout
|
R1 (1kΩ)
|
GND
Même fréquence de coupure: f0 = 1.59 kHz
Comportement:
- Atténuation des basses fréquences
- Gain unitaire (0 dB) aux hautes fréquences
- Pente de +20 dB/décade avant f0
- Déphasage de 0° à +90°
Mesures effectuées:
- Gain à différentes fréquences (tableau de valeurs)
- Phase à différentes fréquences
- Comparaison mesures/théorie
- Impact des composants réels (tolérances)
Supports de cours: Compte rendu TP
TP1: Filtre Sallen-Key
Objectif: Réalisation d’un filtre actif passe-bas du 2ème ordre.
Topologie Sallen-Key unitaire:
Circuit Sallen-Key (gain unitaire):
R1 R2
Ve ----/\/\/\--+-/\/\/\--+-----[AO+]---- Vs
| | | -|
C1 C2 +---+
| |
GND GND
Dimensionnement pour Butterworth:
Pour f0 = 1 kHz et Q = 0.707:
Choix: C1 = C2 = C = 100 nF
R = 1/(2π×f0×C) = 1/(2π × 1000 × 100×10⁻⁹) = 1.59 kΩ
On prend R1 = R2 = 1.6 kΩ (valeur normalisée E24)
Simulation LTspice:
- Analyse AC: diagramme de Bode
- Vérification f0, Q, et pente -40 dB/décade
- Analyse temporelle (réponse indicielle): mesure du dépassement (~4.3% attendu)
- Analyse transitoire avec signal carré: observation de la réponse
Comparaison 1er ordre vs 2ème ordre:
- Sélectivité supérieure du 2ème ordre
- Pente de coupure doublée
- Possibilité de résonance si Q > 0.707
Exercices de TD
TD1: Analyse de filtres passifs
Exercice type: Déterminer la fonction de transfert d’un filtre RC série puis parallèle.
Calcul d’impédances complexes:
Pour un condensateur: Zc = 1/(jCω)
Diviseur de tension: H(jω) = Z2/(Z1 + Z2)
Application numérique: calculer gain et phase pour plusieurs fréquences.
TD2: Amplificateurs opérationnels
Exercice: Dimensionner un amplificateur non-inverseur de gain 10.
H = 1 + (R2/R1) = 10
Donc: R2/R1 = 9
Choix: R1 = 10 kΩ, R2 = 90 kΩ
Vérification de la bande passante:
Pour un AO réel (ex: TL081):
- GBP (Gain-Bandwidth Product) = 3 MHz
- Bande passante à gain 10: fBP = (3×10⁶)/10 = 300 kHz
TD3: Filtres du 2ème ordre
Exercice: Déterminer les valeurs de R et C pour un filtre passe-bas Sallen-Key avec:
- f0 = 10 kHz
- Q = 1 (Bessel)
Méthode:
- Fixer C (ex: 10 nF)
- Calculer R avec ω0 = 1/(RC)
- Ajuster pour obtenir le Q désiré (ratios de résistances/capacités)
TD4: Transformée de Laplace
Exercice: Calculer la réponse temporelle d’un circuit RC à un échelon de tension.
Entrée: Ve(t) = E × u(t) où u(t) est l’échelon unité
En Laplace: Ve(p) = E/p
Fonction de transfert: H(p) = 1/(1 + RCp)
Vs(p) = H(p) × Ve(p) = E/(p×(1 + RCp)) = E/p - (ERC)/(1 + RCp)
Transformée inverse: Vs(t) = E × (1 - exp(-t/(RC))) × u(t)
Constante de temps: τ = RC
À t = τ: Vs(τ) = 0.63E (63% de la valeur finale)
Applications Pratiques
Conditionnement de signaux capteurs:
- Amplification (thermocouples, micros)
- Filtrage anti-repliement avant numérisation (CAN)
- Élimination du bruit 50 Hz (filtre coupe-bande)
Audio:
- Égaliseurs (filtres passe-bande multiples)
- Crossovers pour haut-parleurs (filtres passe-bas/passe-haut)
- Effets (filtres résonants)
Instrumentation:
- Amplificateurs d’instrumentation (gain précis, CMRR élevé)
- Intégrateurs pour capteurs de courant
- Dérivateurs pour capteurs de vitesse
Alimentation:
- Filtrage de l’ondulation résiduelle
- Régulation linéaire avec AO
PART D: ANALYSE ET RÉFLEXION
Connaissances et compétences mobilisées
- Analyse fréquentielle: maîtrise des diagrammes de Bode et de la représentation complexe
- Analyse temporelle: utilisation de la transformée de Laplace pour les réponses transitoires
- Conception de filtres: dimensionnement de filtres actifs et passifs
- Simulation: utilisation de LTspice pour la validation de circuits
- Mesures: utilisation d’oscilloscopes et analyseurs de spectre
- Mathématiques appliquées: nombres complexes, équations différentielles, transformées
Auto-évaluation
Ce cours a été l’un des plus importants de ma formation en électronique analogique.
Points forts:
- Lien théorie/pratique: les TPs avec LTspice ont permis de valider les calculs théoriques
- Outils mathématiques: la transformée de Laplace est un outil puissant pour l’analyse
- Polyvalence: applications dans de nombreux domaines (audio, instrumentation, télécoms)
- Amplificateurs opérationnels: composant universel permettant une grande variété de fonctions
Difficultés rencontrées:
- Mathématiques: manipulations complexes avec les nombres complexes et Laplace
- Dimensionnement: choix des composants (compromis performance/coût/disponibilité)
- Filtres d’ordre supérieur: complexité croissante, difficile à intuiter
Applications pratiques:
- Conception de chaînes d’acquisition de données
- Filtrage de signaux pour systèmes embarqués
- Conditionnement de capteurs analogiques
Mon opinion
Ce cours est fondamental pour tout ingénieur en électronique et systèmes embarqués.
Pourquoi ce cours est essentiel:
- Base de l’électronique analogique: même à l’ère du numérique, l’interface avec le monde réel reste analogique
- Filtrage indispensable: anti-repliement avant CAN, élimination du bruit
- Conditionnement de signaux: amplification, adaptation d’impédance
- Outils réutilisables: Laplace, Bode utilisés dans d’autres cours (automatique, télécoms)
Connexions avec autres cours:
- Filtrage Numérique (S6): équivalent numérique, transformation bilinéaire
- Traitement du Signal (S5): complément théorique (FFT, convolution)
- Chaînes d’Acquisition (S8): application directe pour le conditionnement
- Automatique (S6-S8): même formalisme (Laplace, fonctions de transfert)
Évolution moderne:
Aujourd’hui, les défis sont:
- Mixte analogique-numérique: filtres à capacités commutées, filtres actifs programmables
- Faible consommation: importance pour IoT et objets connectés
- Haute fréquence: défis pour les RF (radio-fréquence)
- Intégration: ASIC, filtres intégrés dans les puces
Outils modernes:
- Filtres numériques: remplacent souvent les filtres analogiques (flexibilité)
- DSP (Digital Signal Processor): traitement tout-numérique
- Mais: filtres analogiques toujours nécessaires en amont du CAN!
Recommandations pour réussir:
- Maîtriser les bases: nombres complexes, équations différentielles
- Pratiquer régulièrement: refaire les TDs, varier les paramètres
- Simuler: LTspice gratuit, expérimenter sans matériel
- Visualiser: tracer les Bode, observer les réponses temporelles
- Comprendre physiquement: ne pas se limiter aux formules
Applications professionnelles:
Ces compétences sont utilisées dans:
- Conception de cartes électroniques: conditionnement de signaux
- Instrumentation: oscilloscopes, multimètres, analyseurs
- Audio professionnel: consoles de mixage, égaliseurs
- Télécommunications: filtrage RF, modulation
- Automobile: capteurs ABS, airbag (critiques)
- Médical: ECG, EEG (amplification de signaux faibles)
- Aéronautique: systèmes critiques, certification
Aspects pratiques importants:
- Choix de l’AO: compromis GBP, slew rate, bruit, offset, coût
- Composants réels: tolérances (±5%, ±10%), dérive en température
- Stabilité: éviter les oscillations (marge de phase, compensation)
- Layout PCB: routage critique (masse, découplage, chemins de retour)
En conclusion, ce cours fournit des bases solides en électronique analogique qui restent pertinentes malgré la montée du numérique. La compréhension des filtres et de l’analyse fréquentielle/temporelle est indispensable pour concevoir des systèmes électroniques complets et performants.
Rapports et Projets
Compte Rendu TP - Circuits et Filtres Analogiques
Rapport de travaux pratiques sur les cellules CR/RC et les filtres Sallen-Key : mesures, simulations LTspice et analyse fréquentielle.