🔄 Systèmes Bouclés - S5
Année: 2022-2023 (Semestre 5)
Crédits: 3 ECTS
Type: Automatique et Régulation
PART A: PRÉSENTATION GÉNÉRALE
Objectifs du cours
Ce cours traite des systèmes asservis (bouclés) en se concentrant sur l’analyse des performances, la stabilité, et la synthèse de correcteurs. L’accent est mis sur les méthodes classiques de l’automatique (PID, correcteurs fréquentiels) et leur application pratique sur des systèmes réels comme les asservissements de position.
Compétences visées
- Comprendre les principes de l’asservissement et du retour d’information
- Analyser la stabilité des systèmes bouclés (Routh, Bode, Nyquist)
- Évaluer les performances temporelles et fréquentielles
- Concevoir des correcteurs PID et à avance/retard de phase
- Utiliser le lieu des racines pour la synthèse
- Maîtriser MATLAB pour la simulation d’asservissements
- Dimensionner des correcteurs selon un cahier des charges
- Analyser les compromis stabilité/rapidité/précision
Organisation
- Volume horaire: Cours magistraux, TD et TP MATLAB
- Évaluation: Examen écrit + TPs
- Semestre: 5 (2022-2023)
- Prérequis: Transformée de Laplace, fonctions de transfert, systèmes linéaires
PART B: EXPÉRIENCE, CONTEXTE ET FONCTION
Contenu pédagogique
Le cours s’articule autour de l’asservissement et de la régulation automatique.
1. Introduction aux systèmes asservis
Principe de l’asservissement:
Un système asservi compare continuellement la sortie (mesurée) à la consigne (référence) et ajuste la commande pour minimiser l’écart (erreur).
Boucle ouverte vs boucle fermée:
| Aspect | Boucle ouverte | Boucle fermée (asservie) |
|---|---|---|
| Structure | Pas de retour | Retour de la sortie |
| Précision | Dépend de la qualité du système | Compense les perturbations |
| Stabilité | Généralement stable | Peut devenir instable |
| Robustesse | Sensible aux variations | Robuste aux perturbations |
| Exemple | Machine à laver | Thermostat |
Avantages de la boucle fermée:
- Réduction de l’erreur statique
- Réjection des perturbations
- Réduction de la sensibilité aux variations de paramètres
- Amélioration de la dynamique
Inconvénients:
- Risque d’instabilité
- Nécessite des capteurs
- Plus complexe à concevoir
Structure générale d’un asservissement:
Composants:
- Consigne (référence): valeur désirée
- Comparateur: calcule l’erreur = consigne - mesure
- Correcteur: élabore la commande à partir de l’erreur
- Actionneur: exécute la commande (moteur, vanne, chauffage)
- Système (procédé): élément à commander
- Capteur: mesure la sortie
- Perturbations: influences externes
2. Analyse temporelle
Caractéristiques de la réponse indicielle:
Pour un échelon en entrée, on observe:
| Paramètre | Notation | Description |
|---|---|---|
| Temps de montée | tm | Temps pour passer de 10% à 90% |
| Temps de réponse | tr | Temps pour rester dans 5% de la valeur finale |
| Dépassement | D | Amplitude du premier pic au-dessus de la valeur finale |
| Temps de pic | tp | Temps pour atteindre le premier pic |
| Erreur statique | eps | Écart permanent entre consigne et sortie |
Systèmes du 1er ordre:
Forme canonique: H(s) = K / (1 + T×s)
Caractéristiques:
- Pas de dépassement
- Temps de réponse à 5%: tr = 3×T
- Constante de temps T détermine la rapidité
Systèmes du 2nd ordre:
Forme canonique: H(s) = omega_n² / (s² + 2×zeta×omega_n×s + omega_n²)
Paramètres:
- omega_n: pulsation naturelle (rapidité)
- zeta: coefficient d’amortissement (oscillations)
Comportement selon zeta:
- zeta > 1: sur-amorti (lent, pas de dépassement)
- zeta = 1: amorti critique (optimal)
- 0 < zeta < 1: sous-amorti (rapide, avec dépassement)
- zeta = 0: oscillations permanentes
Dépassement: D = exp(-pi×zeta / sqrt(1-zeta²))
Pour zeta = 0.7: D ≈ 5% (bon compromis)
Erreur statique:
Dépend de la classe du système en boucle ouverte:
| Classe | Intégrateurs | Erreur échelon | Erreur rampe |
|---|---|---|---|
| 0 | Aucun | eps ≠ 0 | Infinie |
| 1 | 1/s | eps = 0 | eps ≠ 0 |
| 2 | 1/s² | eps = 0 | eps = 0 |
Pour réduire l’erreur statique: ajouter un intégrateur (action I du PID).
3. Stabilité des systèmes bouclés
Définition:
Un système est stable si toute entrée bornée produit une sortie bornée (stabilité BIBO).
Condition: tous les pôles de la fonction de transfert en boucle fermée doivent avoir une partie réelle négative.
Critère de Routh-Hurwitz:
Méthode algébrique pour déterminer la stabilité sans calculer les pôles.
Construction du tableau de Routh à partir du polynôme caractéristique.
Règle: le système est stable si tous les éléments de la première colonne sont strictement positifs.
Avantage: détection de l’instabilité sans résoudre l’équation.
Marges de stabilité:
Marge de gain (Mg):
- Gain supplémentaire admissible avant instabilité
- Mesurée à la pulsation où la phase vaut -180°
- Exprimée en dB
- Mg > 6 dB souhaitable
Marge de phase (Mphi):
- Phase supplémentaire admissible avant instabilité
- Mesurée à la pulsation de coupure (gain = 0 dB)
- Exprimée en degrés
- Mphi > 45° souhaitable
Plus les marges sont grandes, plus le système est robuste.
4. Analyse fréquentielle
Diagrammes de Bode:
Représentation du gain (en dB) et de la phase (en degrés) en fonction de la fréquence (échelle logarithmique).
Gain en dB: G_dB = 20×log10(module de H(jw))
Intérêt:
- Visualiser bande passante
- Lire marges de stabilité
- Concevoir correcteurs graphiquement
Comportements asymptotiques:
| Élément | Gain (dB/décade) | Phase |
|---|---|---|
| Gain K | 20×log(K) | 0° |
| 1/s | -20 | -90° |
| 1/(1+T×s) | 0 puis -20 | 0° puis -90° |
| (1+T×s) | 0 puis +20 | 0° puis +90° |
Pulsation de coupure: fréquence où le gain vaut 0 dB. Liée à la rapidité du système.
Diagramme de Nyquist:
Tracé de H(jw) dans le plan complexe quand w varie de 0 à l’infini.
Critère de Nyquist: Le système bouclé est stable si le point critique (-1, 0) n’est pas encerclé par la courbe.
Distance au point critique: indicateur de robustesse.
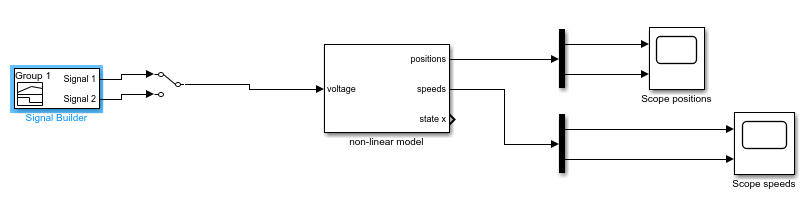
Figure : Simulation d'un système en boucle ouverte (sans retour)
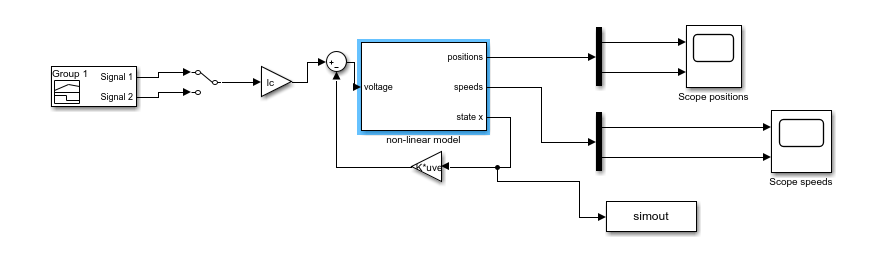
Figure : Système avec retour - amélioration de la stabilité et de la précision

Figure : Réponse d'un système avec correcteur proportionnel
Abaque de Black-Nichols:
Combinaison gain-phase avec courbes iso-gain et iso-phase en boucle fermée.
Permet de lire directement les performances en boucle fermée à partir de la boucle ouverte.
5. Correcteurs classiques
Correcteur Proportionnel (P):
Forme: C(s) = Kp
Effet:
- Réduit l’erreur statique
- Augmente la rapidité
- Peut dégrader la stabilité (diminue marges)
- Ne supprime pas l’erreur statique
Correcteur Proportionnel-Intégral (PI):
Forme: C(s) = Kp × (1 + 1/(Ti×s))
Effet:
- Annule l’erreur statique (intégrateur)
- Améliore la précision
- Dégrade la marge de phase (retard de phase)
- Ralentit légèrement le système
Correcteur Proportionnel-Dérivé (PD):
Forme: C(s) = Kp × (1 + Td×s)
Effet:
- Améliore la stabilité (avance de phase)
- Augmente la rapidité
- Amplifie le bruit haute fréquence
- N’améliore pas l’erreur statique
Correcteur PID:
Forme: C(s) = Kp × (1 + 1/(Ti×s) + Td×s)
Combinaison des trois actions:
- P: action principale, proportionnelle à l’erreur
- I: supprime l’erreur statique
- D: anticipe l’évolution, améliore stabilité
Réglage de Ziegler-Nichols (méthode de la boucle fermée):
- Mettre Ti = infini et Td = 0 (correcteur P)
- Augmenter Kp jusqu’à obtenir des oscillations permanentes
- Noter Kp_critique et période d’oscillation Tu
- Calculer les paramètres selon le type:
| Type | Kp | Ti | Td |
|---|---|---|---|
| P | 0.5×Kp_critique | - | - |
| PI | 0.45×Kp_critique | 0.83×Tu | - |
| PID | 0.6×Kp_critique | 0.5×Tu | 0.125×Tu |
Correcteur à avance de phase:
Forme: C(s) = K × (1 + a×T×s) / (1 + T×s) avec a > 1
Effet:
- Apporte une avance de phase (améliore marge de phase)
- Augmente la rapidité
- Permet de stabiliser un système instable
Utilisé quand: marge de phase insuffisante ou système trop lent.
Correcteur à retard de phase:
Forme: C(s) = K × (1 + T×s) / (1 + a×T×s) avec a > 1
Effet:
- Augmente le gain basse fréquence
- Réduit l’erreur statique
- Peu d’impact sur la dynamique
Utilisé quand: erreur statique trop importante.
6. Lieu des racines
Principe:
Représentation graphique des pôles en boucle fermée quand un paramètre (généralement le gain K) varie de 0 à l’infini.
Utilité:
- Visualiser l’évolution de la stabilité
- Choisir le gain pour placer les pôles
- Identifier les zones de stabilité
- Concevoir des compensateurs
Règles de construction:
- Commence aux pôles de H(s) en boucle ouverte (K=0)
- Se termine aux zéros de H(s) (K→∞) ou à l’infini
- Nombre de branches = nombre de pôles
- Symétrie par rapport à l’axe réel
- Asymptotes vers l’infini
Pôles dominants:
Pôles les plus proches de l’axe imaginaire, qui gouvernent principalement la dynamique.
Les pôles éloignés ont moins d’influence sur la réponse temporelle.
Permet de simplifier l’analyse en ne considérant que les pôles dominants.
PART C: ASPECTS TECHNIQUES
Travaux Pratiques
TP: Asservissement de position d’un bras
Objectif: concevoir un asservissement de position pour un système mécanique.
Système typique: bras robotique avec moteur DC.
Étapes du TP:
- Modélisation: obtenir la fonction de transfert du système
- Analyse en boucle ouverte: stabilité, performances
- Étude en boucle fermée: avec correcteur proportionnel
- Conception de correcteur: PID ou avance de phase
- Simulation: validation avec MATLAB/Simulink
- Évaluation: vérification du cahier des charges
Cahier des charges typique:
- Temps de réponse < 0.5 s
- Dépassement < 10%
- Erreur statique nulle
- Marge de phase > 45°
- Rejet de perturbations
Outils MATLAB
Fonctions de base:
% Définir fonction de transfert
num = [1];
den = [1 2 1];
H = tf(num, den);
% Boucle fermée
Hbf = feedback(H, 1);
% Réponse indicielle
step(Hbf);
grid;
% Diagrammes de Bode
bode(H);
margin(H); % Avec marges
% Lieu des racines
rlocus(H);
% Nyquist
nyquist(H);
% Pôles et zéros
pole(H)
zero(H)
Conception de correcteur PID:
% Correcteur PID manuel
Kp = 10;
Ki = 5;
Kd = 2;
C = pid(Kp, Ki, Kd);
% Système corrigé
Hcorrige = C * H;
Hbf = feedback(Hcorrige, 1);
% Validation
step(Hbf);
% Réglage automatique
C_auto = pidtune(H, 'PID');
Analyse de performances:
% Informations sur la réponse
info = stepinfo(Hbf);
% Contient: RiseTime, SettlingTime, Overshoot, etc.
% Marges de stabilité
[Gm, Pm, Wcg, Wcp] = margin(H);
fprintf('Marge de phase: %.1f degrés\n', Pm);
fprintf('Marge de gain: %.1f dB\n', 20*log10(Gm));
Travaux Dirigés
TD1: Systèmes du 1er et 2nd ordre
Exercices sur:
- Calcul de constantes de temps
- Détermination de paramètres (zeta, omega_n)
- Calcul de dépassement et temps de réponse
- Identification à partir de réponse temporelle
TD2: Stabilité et précision
Problématiques:
- Application du critère de Routh
- Détermination de plage de gains stables
- Calcul d’erreurs statiques
- Choix de correcteurs selon spécifications
TD3: Analyse fréquentielle
Exercices sur:
- Tracé de diagrammes de Bode asymptotiques
- Lecture de marges de stabilité
- Interprétation de Nyquist
- Conception graphique de correcteurs
TD4: Synthèse de correcteurs
Applications:
- Réglage de PID par Ziegler-Nichols
- Dimensionnement de correcteur à avance de phase
- Utilisation du lieu des racines
- Validation de cahier des charges
Méthodologie de conception
Démarche type:
- Analyse du système: fonction de transfert, pôles, zéros
- Spécifications: traduire cahier des charges en contraintes techniques
- Choix du correcteur: selon défauts à corriger
- Dimensionnement: calcul des paramètres (Kp, Ki, Kd, a, T)
- Simulation: validation avec MATLAB
- Ajustement: itérations si nécessaire
- Robustesse: test avec variations de paramètres
Compromis à gérer:
| Objectif | Compromis |
|---|---|
| Rapidité vs Stabilité | Gain élevé accélère mais déstabilise |
| Précision vs Robustesse | Gain élevé améliore précision mais réduit marges |
| Filtrage du bruit vs Rapidité | Dérivée amplifie le bruit |
Règles pratiques:
- Commencer par un P, ajouter I si erreur statique
- Ajouter D si dépassement trop important
- Vérifier marges: Mphi > 45°, Mg > 6 dB
- Tester robustesse avec ±20% de variations
PART D: ANALYSE ET RÉFLEXION
Compétences acquises
Analyse:
- Évaluation de performances temporelles (tr, D, eps)
- Détermination de stabilité (Routh, marges)
- Interprétation de diagrammes fréquentiels
- Identification de systèmes par expérimentation
Conception:
- Choix de correcteur adapté au problème
- Dimensionnement de PID
- Synthèse par méthodes fréquentielles
- Optimisation de compromis
Outils:
- Maîtrise de MATLAB/Simulink pour l’automatique
- Utilisation de diagrammes (Bode, Nyquist, lieu racines)
- Simulation et validation de lois de commande
Applications industrielles
Les systèmes asservis sont omniprésents dans l’industrie:
Procédés industriels:
- Régulation de température (fours, réacteurs)
- Contrôle de pression (compresseurs, cuves)
- Régulation de débit (pompes, vannes)
- Contrôle de niveau (réservoirs)
Robotique:
- Asservissement de position des articulations
- Contrôle de trajectoire
- Stabilisation (robots équilibrés, drones)
- Contrôle de force (préhension, assemblage)
Automobile:
- Régulateur de vitesse (cruise control)
- ABS (antiblocage de roues)
- ESP (contrôle de stabilité)
- Suspension active
Aéronautique:
- Pilote automatique
- Contrôle d’attitude (tangage, roulis, lacet)
- Régulation de poussée
- Commandes de vol électriques
Électronique de puissance:
- Alimentations à découpage régulées
- Onduleurs pour moteurs
- Redresseurs actifs
- Batteries et chargeurs
Liens avec autres cours
| Cours | Lien |
|---|---|
| Modélisation Systèmes Linéaires (S5) | Représentation d’état, observateurs |
| Systèmes Linéaires Continus (S5) | Fonctions de transfert, Laplace |
| Circuits Analogiques (S5) | Filtres, correcteurs analogiques |
| Électronique de Puissance (S6) | Asservissement de convertisseurs |
| Commande Numérique (S8) | Discrétisation, PID numérique |
| Temps Réel (S8) | Implémentation de régulateurs |
Différences avec autres cours d’automatique
Systèmes Bouclés vs Systèmes Linéaires:
| Aspect | Systèmes Bouclés | Systèmes Linéaires |
|---|---|---|
| Focus | Asservissement, correcteurs | Représentation d’état |
| Méthodes | Fréquentielles (Bode, Nyquist) | Temporelles (placement pôles) |
| Outils | PID, lieu racines | Retour d’état, observateurs |
| Approche | Classique, industrielle | Moderne, théorique |
Complémentarité:
- Systèmes Bouclés: pratique industrielle immédiate (PID)
- Systèmes Linéaires: théorie moderne pour systèmes complexes
Évolution et perspectives
Commande avancée:
Les méthodes classiques restent majoritaires en industrie mais sont complétées par:
Commande optimale: LQR, LQG (minimisation de critère)
Commande robuste: H-infini, mu-synthèse (incertitudes)
Commande adaptative: ajustement automatique des paramètres
Commande prédictive: MPC (Model Predictive Control)
Intelligence artificielle:
- Réseaux de neurones pour identification
- Apprentissage par renforcement pour optimisation
- Contrôle flou (fuzzy logic)
Industrie 4.0:
- Supervision et monitoring en temps réel
- Maintenance prédictive
- Optimisation énergétique
- Jumeau numérique
Mon opinion
Ce cours est essentiel pour comprendre comment fonctionne la régulation automatique dans les systèmes réels.
Points forts:
- Approche pratique et industrielle
- Outils immédiatement utilisables (PID)
- Méthodes graphiques intuitives (Bode)
- TPs concrets avec systèmes physiques
Complémentarité:
Le PID reste le correcteur le plus utilisé industriellement (>90% des boucles de régulation). Sa simplicité et son efficacité en font un outil incontournable.
La compréhension des compromis stabilité/rapidité/précision est fondamentale pour toute conception de système automatique.
Applications concrètes:
Les notions apprises s’appliquent directement à:
- Thermostat domestique (régulation température)
- Régulateur de vitesse automobile
- Drones et stabilisation
- Robots industriels
- Procédés chimiques
Importance professionnelle:
La maîtrise des asservissements est recherchée dans:
- Automatisation industrielle
- Robotique
- Aéronautique
- Automobile
- Électronique de puissance
- Systèmes embarqués
Lien avec la pratique:
Ce cours prépare à:
- Régler des régulateurs industriels
- Diagnostiquer problèmes d’instabilité
- Optimiser performances de boucles existantes
- Concevoir nouvelles régulations
Bilan personnel: Ce cours a fourni les outils classiques de l’automatique industrielle. La compréhension du PID et des méthodes fréquentielles est directement applicable en contexte professionnel. La combinaison avec le cours de représentation d’état offre une vision complète de l’automatique moderne. Les TPs sur systèmes réels (asservissement de position) ont permis de confronter théorie et pratique, révélant l’importance des compromis et de la robustesse dans les applications concrètes.
📚 Documents de Cours
Voici les supports de cours en PDF pour approfondir les systèmes bouclés :
📖 Chapitre 1 - Fondamentaux
Introduction aux systèmes bouclés, concepts de base de l'automatique et premières notions de commande.
📊 Chapitre 2 - Analyse et Synthèse
Analyse fréquentielle, stabilité, marges de gain et de phase, méthodes de synthèse de correcteurs.
📈 Chapitre 3 - Diagrammes de Bode
Tracé et analyse des diagrammes de Bode, identification de systèmes et réglage de correcteurs.