Energie - S2

PART A : PRESENTATION GENERALE

Contexte et objectifs

Le cours d’Energie au semestre 2 du DUT GEII approfondit les concepts d’electrotechnique abordes au S1. Il se concentre sur trois piliers fondamentaux de la conversion d’energie electrique : les systemes triphases, les machines a courant continu (MCC) et les transformateurs monophases. Ces notions sont essentielles pour tout ingenieur travaillant dans le domaine de la distribution electrique, de la motorisation industrielle ou des systemes de puissance.

Objectifs pedagogiques :

• Comprendre et analyser les systemes triphases equilibres (tensions, courants, puissances)
• Maitriser le fonctionnement et la modelisation des machines a courant continu
• Etudier les transformateurs monophases (ideal, reel, essais normalises)
• Realiser des bilans de puissance et calculer des rendements
• Appliquer les methodes de mesure de puissance en triphase (methode des deux wattmetres)

Organisation

Le cours est structure en trois grands modules : systemes triphases, machines a courant continu et transformateurs. Chaque module comprend des cours magistraux (CM), des travaux diriges (TD) et des travaux pratiques (TP) sur bancs d’essai reels. Les TP permettent de manipuler des machines electriques et de realiser des mesures de puissance avec des wattmetres, des ampere-metres et des voltmetres.

PART B : EXPERIENCE ET CONTEXTE

Environnement pedagogique

L’enseignement d’Energie S2 s’inscrit dans la continuite du S1 qui avait introduit les bases de l’electricite et de l’electrotechnique. Le contexte sanitaire de l’annee 2020-2021 a impose certaines adaptations, avec une partie de l’enseignement a distance, mais les TP ont pu etre maintenus en presentiel pour permettre la manipulation des machines electriques et des instruments de mesure.

Outils et equipements utilises

• Bancs d’essai machines : moteurs a courant continu, transformateurs monophases, alternateur triphase
• Instruments de mesure : wattmetres, ampere-metres, voltmetres, oscilloscope pour visualiser les tensions triphases
• Logiciel de simulation : PSIM pour la simulation de circuits de puissance
• Calculatrice scientifique : calculs de puissance, facteur de puissance, rendements

Liens avec d’autres cours

Ce cours est etroitement lie a plusieurs enseignements du DUT GEII :

• Mathematiques S2 : les equations differentielles et les nombres complexes sont utilises pour l’analyse des circuits en regime sinusoidal
• Outils Logiciels (OL) : la transformation de Laplace aide a modeliser les systemes electriques
• Systemes Electroniques (SE) : les quadripoles et la representation frequentielle s’appliquent aux transformateurs
• ER S2 : la conception de circuits d’interface inclut des alimentations qui utilisent des transformateurs

PART C : ASPECTS TECHNIQUES

1. Systemes triphases equilibres

1.1 Principe et generation

Un systeme triphase equilibre est constitue de trois tensions sinusoidales de meme amplitude et de meme frequence, dephasees de 120 degres (2pi/3 radians) les unes par rapport aux autres. Ce systeme est produit par un alternateur triphase dont le stator comporte trois enroulements decales de 120 degres.

Les trois tensions simples (entre phase et neutre) s’ecrivent :

V1(t) = Vmax * sin(omega * t)
V2(t) = Vmax * sin(omega * t - 2*pi/3)
V3(t) = Vmax * sin(omega * t - 4*pi/3)

Ou Vmax est l’amplitude maximale et omega = 2*pi*f la pulsation (f = 50 Hz en Europe).

Propriete fondamentale : la somme des trois tensions simples est nulle a tout instant :

V1(t) + V2(t) + V3(t) = 0

Cette propriete permet de ne pas utiliser de fil neutre dans un systeme equilibre, ce qui represente une economie de cuivre significative dans le transport d’electricite.

1.2 Tensions composees (ligne a ligne)

Les tensions composees (ou tensions entre phases) se deduisent des tensions simples :

U12 = V1 - V2
U23 = V2 - V3
U31 = V3 - V1

La relation fondamentale entre tension composee U et tension simple V est :

U = sqrt(3) * V

En valeurs efficaces, si V = 230 V (tension simple du reseau domestique), alors U = 230 * sqrt(3) = 400 V (tension composee).

1.3 Couplages etoile et triangle

Couplage etoile (Y) : les trois recepteurs sont connectes entre chaque phase et le neutre. Chaque recepteur est soumis a la tension simple V. Le courant de ligne est egal au courant dans le recepteur.

I_ligne = I_phase
U_recepteur = V (tension simple)

Couplage triangle (Delta) : les trois recepteurs sont connectes entre deux phases. Chaque recepteur est soumis a la tension composee U. Le courant de ligne est sqrt(3) fois le courant dans le recepteur.

I_ligne = sqrt(3) * I_phase
U_recepteur = U (tension composee)

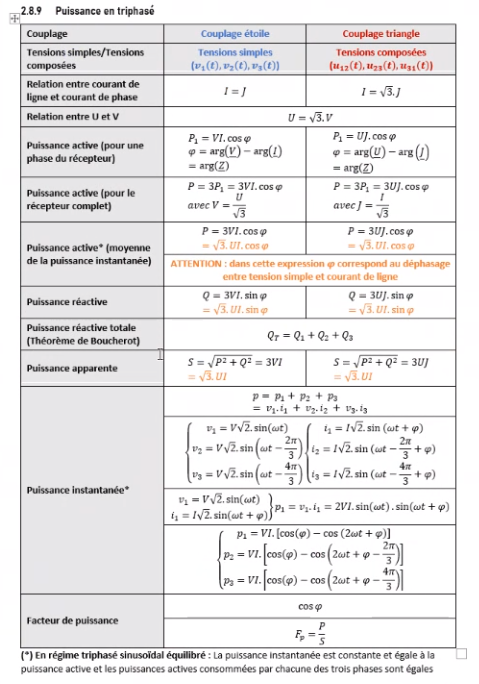
1.4 Puissances en triphase

Pour un systeme triphase equilibre, les puissances s’expriment de facon symetrique :

Puissance active (en Watts) :

P = sqrt(3) * U * I * cos(phi)

Puissance reactive (en VAR) :

Q = sqrt(3) * U * I * sin(phi)

Puissance apparente (en VA) :

S = sqrt(3) * U * I

Ou phi est le dephasage entre la tension et le courant dans chaque phase, U la tension composee efficace et I le courant de ligne efficace.

Facteur de puissance :

cos(phi) = P / S

Le facteur de puissance est un indicateur essentiel de l’efficacite d’une installation electrique. Un facteur de puissance faible (proche de 0) signifie que l’installation consomme beaucoup de puissance reactive sans produire de travail utile. Les fournisseurs d’electricite penalisent les installations ayant un cos(phi) inferieur a 0.93.

1.5 Mesure de puissance : methode des deux wattmetres

En triphase equilibre sans neutre, la puissance active peut etre mesuree avec seulement deux wattmetres (methode d’Aron) :

P_totale = W1 + W2

Ou :
W1 = U13 * I1 * cos(angle entre U13 et I1)
W2 = U23 * I2 * cos(angle entre U23 et I2)

On peut aussi en deduire la puissance reactive :

Q_totale = sqrt(3) * (W1 - W2)

Et le facteur de puissance :

tan(phi) = sqrt(3) * (W1 - W2) / (W1 + W2)

2. Machine a courant continu (MCC)

2.1 Principe de fonctionnement

La machine a courant continu est une machine electrique tournante qui convertit l’energie electrique en energie mecanique (moteur) ou inversement (generatrice). Son fonctionnement repose sur la loi de Laplace (force exercee sur un conducteur parcouru par un courant dans un champ magnetique) et la loi de Faraday (induction d’une f.e.m. dans un conducteur en mouvement dans un champ magnetique).

La machine se compose de deux parties :

• Le stator (inducteur) : cree le champ magnetique B (soit par des aimants permanents, soit par des bobines d’excitation)
• Le rotor (induit) : comporte les conducteurs dans lesquels circule le courant d’induit

Le collecteur et les balais permettent de convertir le courant alternatif induit dans les spires du rotor en courant continu aux bornes de la machine.

2.2 Equations fondamentales

Force electromotrice (f.e.m.) :

E = K * Phi * Omega

Ou :

• E est la f.e.m. induite (en Volts)
• K est une constante de construction (depend du nombre de conducteurs, du nombre de paires de poles)
• Phi est le flux magnetique par pole (en Webers)
• Omega est la vitesse angulaire du rotor (en rad/s)

On ecrit aussi : E = K' * Phi * N avec N la vitesse en tr/min et K’ une constante adaptee.

Couple electromagnetique :

C = K * Phi * I

Ou I est le courant d’induit (en Amperes) et C le couple electromagnetique (en N.m).

Le produit K*Phi est souvent note k et correspond a la constante de couple/vitesse de la machine. On a la relation importante :

E = k * Omega
C = k * I

Avec la meme constante k, ce qui traduit la dualite electromecanique de la machine.

2.3 Schema equivalent et equation electrique

Le modele electrique de l’induit d’une MCC en regime permanent est :

U = E + R * I     (en moteur)
U = E - R * I     (en generatrice)

Ou :

• U est la tension aux bornes de l’induit
• E est la f.e.m. (E = K * Phi * Omega)
• R est la resistance de l’induit (bobinage + balais)
• I est le courant d’induit

En substituant l’expression de E :

U = K * Phi * Omega + R * I

D’ou la vitesse de rotation :

Omega = (U - R * I) / (K * Phi)

Et le courant de demarrage (Omega = 0, donc E = 0) :

I_demarrage = U / R

Ce courant est tres eleve (5 a 10 fois le courant nominal), ce qui impose l’utilisation de resistances de demarrage ou de variateurs.

2.4 Caracteristique couple-vitesse

En eliminant I entre les equations electrique et de couple :

Omega = U / (K * Phi) - (R / (K * Phi)^2) * C

Cette relation montre que la caracteristique Omega(C) est une droite decroissante (en excitation separee). A vide (C = 0), la vitesse est maximale. En charge, la vitesse diminue legerement a cause de la chute de tension R*I dans l’induit.

2.5 Bilan de puissance

Le bilan de puissance de la MCC en fonctionnement moteur s’ecrit :

P_absorbee = U * I                    (puissance electrique absorbee)
P_Joule = R * I^2                      (pertes Joule dans l'induit)
P_electromagnetique = E * I = C * Omega (puissance convertie)
P_mecanique = C_utile * Omega          (puissance mecanique utile)
P_pertes_mecaniques = P_fer + P_frottement (pertes fer + frottement)

Le rendement du moteur :

eta = P_utile / P_absorbee = (U*I - R*I^2 - P_pertes) / (U*I)

3. Transformateurs monophases

3.1 Principe et constitution

Le transformateur monophase est un convertisseur statique d’energie electrique qui permet de modifier la valeur d’une tension alternative. Il est constitue de :

• Un circuit magnetique (noyau en toles ferromagnetiques feuilletees pour limiter les courants de Foucault)
• Un enroulement primaire de N1 spires
• Un enroulement secondaire de N2 spires

Le principe repose sur l’induction electromagnetique mutuelle : le courant alternatif dans le primaire cree un flux magnetique variable qui traverse le secondaire et y induit une f.e.m.

3.2 Transformateur ideal

Le transformateur ideal est un modele theorique ou :

• Il n’y a aucune perte (ni Joule, ni fer)
• Le couplage magnetique est parfait (pas de fuites)
• La permeabilite du noyau est infinie

Dans ce cas, le rapport de transformation m est :

m = N2 / N1 = V2 / V1 = I1 / I2

Ou :

• N1, N2 : nombres de spires du primaire et du secondaire
• V1, V2 : tensions efficaces au primaire et au secondaire
• I1, I2 : courants efficaces au primaire et au secondaire

La puissance est integralement transmise : S1 = V1 * I1 = V2 * I2 = S2

Si m > 1, le transformateur est elevateur de tension. Si m < 1, il est abaisseur.

3.3 Transformateur reel : modele de Boucherot

Le transformateur reel presente des imperfections qui sont modelisees par le schema equivalent de Boucherot :

Pertes fer (dans le noyau) :

• Pertes par hysteresis : proportionnelles a f * Bmax^2
• Pertes par courants de Foucault : proportionnelles a f^2 * Bmax^2
• Totale : P_fer = constante (ne depend pas de la charge)
• Modelisees par une resistance Rf en parallele avec le primaire

Pertes Joule (dans les enroulements) :

• Au primaire : P_J1 = R1 * I1^2
• Au secondaire : P_J2 = R2 * I2^2
• Ces pertes dependent du courant (donc de la charge)

Fuites magnetiques :

• Modelisees par des inductances de fuite L1 et L2
• En regime sinusoidal : reactances de fuite X1 = L1omega et X2 = L2omega

Le schema equivalent ramene au secondaire utilise l’impedance totale ramenee :

Rs = R2 + R1 * m^2     (resistance totale ramenee au secondaire)
Xs = X2 + X1 * m^2     (reactance totale ramenee au secondaire)
Zs = Rs + j*Xs          (impedance totale ramenee au secondaire)

3.4 Essai a vide

L’essai a vide consiste a alimenter le primaire sous tension nominale V1n avec le secondaire ouvert (I2 = 0). On mesure :

V1 = V1n (tension nominale au primaire)
V20 (tension a vide au secondaire)
I10 (courant a vide au primaire)
P10 (puissance a vide absorbee)

Cet essai permet de determiner :

• Le rapport de transformation : m = V20 / V1n
• Les pertes fer : P_fer = P10 - R1 * I10^2 (on neglige souvent R1*I10^2 car I10 est tres faible)
• Donc en pratique : P_fer ≈ P10

3.5 Essai en court-circuit

L’essai en court-circuit consiste a court-circuiter le secondaire et a alimenter le primaire sous tension reduite V1cc (pour que le courant atteigne sa valeur nominale). On mesure :

V1cc (tension reduite au primaire)
I2cc = I2n (courant nominal au secondaire)
P1cc (puissance absorbee en court-circuit)

Cet essai permet de determiner :

• Les pertes Joule nominales : P_Joule = P1cc (les pertes fer sont negligeables car V1cc « V1n)
• L’impedance ramenee : Zs = V1cc * m / I2n
• La resistance ramenee : Rs = P1cc * m^2 / I2n^2
• La reactance ramenee : Xs = sqrt(Zs^2 - Rs^2)

3.6 Rendement et chute de tension

La chute de tension au secondaire en charge s’ecrit (formule approchee) :

Delta_V2 = Rs * I2 * cos(phi2) + Xs * I2 * sin(phi2)
V2 = V20 - Delta_V2

Le rendement du transformateur :

eta = P2 / P1 = (V2 * I2 * cos(phi2)) / (V2 * I2 * cos(phi2) + P_fer + Rs * I2^2)

Le rendement maximal est atteint lorsque les pertes Joule sont egales aux pertes fer :

Rs * I2^2 = P_fer  =>  I2_optimal = sqrt(P_fer / Rs)

4. Exemple d’application : dimensionnement

Probleme : Un moteur MCC fonctionne sous U = 220 V, avec une resistance d’induit R = 0.5 Ohm et une constante k = K*Phi = 1.2 V.s/rad. On souhaite determiner la vitesse et le courant pour un couple utile de 30 N.m (en negligeant les pertes mecaniques).

Resolution :

Couple : C = k * I  =>  I = C / k = 30 / 1.2 = 25 A
Equation electrique : U = E + R * I = k * Omega + R * I
Omega = (U - R * I) / k = (220 - 0.5 * 25) / 1.2
Omega = 207.5 / 1.2 = 172.9 rad/s
N = Omega * 60 / (2 * pi) = 1651 tr/min
Rendement : eta = E * I / (U * I) = (k * Omega * I) / (U * I)
eta = (1.2 * 172.9) / 220 = 207.5 / 220 = 94.3%

PART D : ANALYSE ET REFLEXION

Competences acquises

Ce cours m’a permis de developper des competences solides en electrotechnique :

• Analyse de systemes triphases : capacite a calculer les tensions, courants et puissances dans un systeme triphase equilibre, en distinguant les couplages etoile et triangle. La methode des deux wattmetres pour la mesure de puissance est un outil pratique que j’ai pu appliquer en TP.

• Modelisation de machines electriques : comprehension du fonctionnement de la MCC a travers son modele equivalent, ses equations fondamentales et sa caracteristique couple-vitesse. La capacite a realiser un bilan de puissance complet est essentielle pour le dimensionnement.

• Etude des transformateurs : maitrise du modele de Boucherot, des essais a vide et en court-circuit, et du calcul de rendement. Ces competences sont directement applicables dans le domaine de la distribution electrique.

Auto-evaluation

La partie triphase a ete bien assimilee grace a la regularite des equations et aux nombreux exercices. La MCC a necessite un effort de comprehension pour bien saisir la dualite entre les grandeurs electriques et mecaniques. Les transformateurs, avec leur schema equivalent de Boucherot, ont ete le module le plus exigeant en termes de modelisation.

Les TP ont ete particulierement enrichissants car ils permettaient de confronter les calculs theoriques aux mesures reelles, avec les incertitudes et les imperfections des machines reelles.

Connexions et applications

Les connaissances acquises dans ce cours trouvent des applications directes dans :

• L’industrie : dimensionnement de moteurs, choix de transformateurs, compensation du facteur de puissance
• Les energies renouvelables : les eoliennes utilisent des generatrices (synchrones ou asynchrones), les panneaux solaires necessitent des convertisseurs
• Les transports : les vehicules electriques utilisent des machines electriques (souvent synchrones a aimants permanents)
• La distribution electrique : le reseau de transport utilise des transformateurs pour elever/abaisser la tension

Ce cours est fondamental pour la suite du cursus, notamment les cours de S3-S4 qui abordent l’electronique de puissance et les convertisseurs statiques.

Documents de Cours